Bubble Sort Is Not Robust Either
Just after I published the previous article on bubble sort, I stumbled over another account claiming bubble sort is somehow more robust than better algorithms (emphasis mine):1 I should clarify that I generally agree with the author’s sentiment. It’s just this example that’s wrong and triggering to me.
To see how robustness and efficiency can trade off, consider sorting a list by comparing pairs of items. […] Efficient sorting algorithms make comparisons that often move items long distances. Bubble sort doesn’t do that. It compares items one position at a time. […]
Imagine that comparison is unreliable. For this demonstration, the comparison usually works fine, but on 10 % of comparisons it gives a random answer. It might claim 3 > 7, or 12 = 9, or whatever.
Averaged over 1,000 shuffles, here are the errors made by each sorting algorithm:
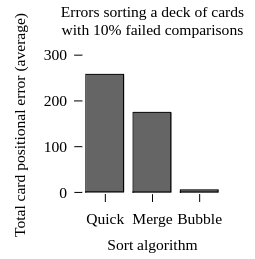
Now whose doors have fallen off? Bubble sort’s inefficient repeated comparisons repair many faults, and its inefficient short moves minimize the damage of the rest.
This is just not true. There is a much simpler explanation.
Think about it: what is the last thing bubble sort does before it hands back a sorted sequence? It scans through the sequence and verifies it is in order.
Bubble sort has to do this, because it is very myopic and cannot otherwise know when it has finished sorting. This exit condition of bubble sort is what provides all of the reliability the author discovers. Not the “inefficient short moves” or the “repeated comparisons”.
We can verify this quite easily: we add the same exit condition to insertion sort. If we do, and run the same experiment as the author, we get the following results:
| Algorithm | Mean card positional error |
|---|---|
| Plain insertion sort | 800 |
| Bubble sort | 1.84 |
| Checked insertion sort | 0.16 |
Now whose doors have fallen off? Not only is the checked insertion sort much more efficient, it is also over ten times as robust.
I’m still not entirely sure why insertion sort is more robust, but my guess is that it mainly happens at the end, when the sequence is very nearly sorted. Because bubble sort only moves elements one spot at a time, it gets a lot more opportunities to mistakenly declare the sequence sorted when there is still one element that needs to be nudged into place.
Insertion sort, being more efficient, does not suffer from this problem.
A reader pointed out that there is a long-standing class of sorting algorithms that is designed to work with sloppy comparison functions: game tournaments! A match in a game is a comparison that frequently generates the wrong result, and good tournament designs should produce somewhat robust results despite that.2 Knockout designs are the worst.
Of course, tournaments are also designed so that each participating element undergoes roughly the same number of comparisons3 Except knockout designs. Again, they are the worst! which is something we don’t have to account for in sorting algorithms, but it was still interesting to hear the analogy. As obvious as it seems in hindsight, I had not thought about that before.
Appendix A: Implementations
The premise of this article is based on a false assumption: I had assumed David Ackley had implemented the typical, optimised bubble sort that exits early once the list is sorted. If one looks at his implementation, it turns out that’s not at all how it works. It naïvely goes through all n iterations! Here it is:
sub bsort { my (@data) = @_; my $n = scalar(@data); for (1 .. $n) { for (my $j = 0; $j < $n-1; ++$j) { local($a) = $data[$j]; local($b) = $data[$j+1]; if (dcmpRaw() > 0) { # NOTE bsort uses dcmpRaw always! No armoring! my $t = $data[$j+1]; $data[$j+1] = $data[$j]; $data[$j] = $t; } } } return @data; }
In contrast, I used the following implementation, which contains the optimisation that ducks out early if the list appears sorted – which also causes it to run more than n iterations if the list continues to appear unsorted!
sub bubble { my ($p, @xs) = @_; while (1) { my $ordered = 1; for (my $i = 0; $i < $#xs; $i++) { # Faulty comparison returns the wrong result $p percent of the time. if (rand() < $p ? $xs[$i] < $xs[$i+1] : $xs[$i+1] < $xs[$i]) { $ordered = 0; ($xs[$i+1], $xs[$i]) = ($xs[$i], $xs[$i+1]); } } last if $ordered; } return @xs; }
Despite that difference, this article resulted in a lot of interesting discussion, so I’m keeping it up as it is. This is the regular insertion sort I used:
sub insertion { my ($p, @xs) = @_; for (my $i = 0; $i < @xs; $i++) { # We know everything up to but excluding $i is in order. # I.e. index $i is the next to be sorted. my $x = $xs[$i]; # Faulty comparison returns the wrong result $p percent of the time. if (rand() < $p ? $xs[$i-1] < $x : $x < $xs[$i-1]) { # Find the right place for $x, shifting as we go. for (my $j = $i-1; $j >= -1; $j--) { # Faulty comparison returns the wrong result $p percent of the time. if ($j >= 0 && (rand() < $p ? $xs[$j] < $x : $x < $xs[$j])) { $xs[$j+1] = $xs[$j]; } else { $xs[$j+1] = $x; last; } } } } return @xs; }
The checked insertion sort is almost the same except it is wrapped in an
infinite loop and sets $ordered to false if an unordered element is detected.
sub insertion_checked { my ($p, @xs) = @_; while (1) { my $ordered = 1; for (my $i = 0; $i < @xs; $i++) { # We know everything up to but excluding $i is in order. # I.e. index $i is the next to be sorted. my $x = $xs[$i]; # Faulty comparison returns the wrong result $p percent of the time. if (rand() < $p ? $xs[$i-1] < $x : $x < $xs[$i-1]) { $ordered = 0; # Find the right place for $x, shifting as we go. for (my $j = $i-1; $j >= -1; $j--) { # Faulty comparison returns the wrong result $p percent of the time. if ($j >= 0 && (rand() < $p ? $xs[$j] < $x : $x < $xs[$j])) { $xs[$j+1] = $xs[$j]; } else { $xs[$j+1] = $x; last; } } } } last if $ordered; } return @xs; }
The function that computes the distance and simultaneously verifies that all elements exist in the sorted sequence4 This rules out many silly bugs in the implementations of the sort routines. is
sub distance { my (@xs) = @_; my $s = 0; my %encountered = (); for my $i (0..$#xs) { $encountered{$xs[$i]}++; $s += abs(($i + 1) - $xs[$i]); } for my $i (1..52) { if ($encountered{$i} != 1) { say "Found uhh, $encountered{$i} of $i..."; } } return $s; }
We get the distributions of errors with
my $B = 1000; say 'bubble,insertion,ins_checked'; for my $i (1..$B) { my @deck = shuffle(1..52); my $b = distance bubble(0.1, @deck); my $i = distance insertion(0.1, @deck); my $c = distance insertion_checked(0.1, @deck); say "$b,$i,$c"; }