Emptying the Dishwasher With Systems Theory
We have talked previously about the flows of information in systems. This time, we’ll look into the flows of material.
Summary
- Systems concerning transport of material consist essentially of flows and current counts in various locations. “Transport” and “material” are to be interpreted extremely broadly: a bug tracker transports material: bug tickets are transported in and out of the open state.
- Rates of flow are more important than current counts. It’s great that you have money in your bank account, but if you spend more than you earn, it’s going to run out eventually.
- In the (often not-so-)long run, one-time changes are drowned out by ongoing flows. If your well is drying up, you might get someone to refill it, but if you change nothing else, it will dry up again soon enough.
- On a limited budget, it pays to quickly get to a point where flows are rearranged so that time is on your side. After that, you can work as slowly as whatever remaining budget allows.
- In any imbalance of flows, there’s two sides, and you can leverage that to find counter-intuitive solutions. Maybe the problem of expensive meat is not to produce more meat, but to encourage people to consume less of it.
The Dishwasher System
This article pretends to be about dishwashers, but it’s really about something much more general.
After your dishwasher has finished, when it contains clean dishes, you don’t want to put dirty dishes in there.1 At least that’s how every I’ve met does it – if you have a process that allows dirty and clean dishes coexist in the dishwasher, you need to tell me about it! However, your household will continue produce dirty dishes at a rate which you cannot directly control – these will collect at the counter, waiting for the dishwasher to be emptied.
The one thing you can control is how much effort you put into maintaining the dishwasher system. This work either has the effect of transferring clean dishes out of the dishwasher into cabinets (if the dishwasher contains clean dishes), or transferring dirty dishes from the counter to the dishwasher (in the other case).
Let’s visualise these two states of the system. First up is the emptying state, when the dishwasher contains clean dishes. The grey arrow indicates a transfer of dishes you don’t have direct control over: your household dirties dishes at the rate they are used to. The black arrow is the one you can control: how fast you refill the cabinets with clean dishes from the dishwasher.2 The attentive reader will note that there are really two transfers from the dishwasher going on in this state: the household is likely taking clean dishes from the dishwasher in addition to the cabinets, and this is independent of your effort. I have excluded this from the model with no loss of utility because it just complicates the analysis for no qualitative difference.
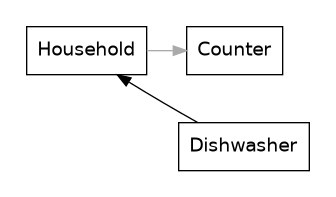
Then we have the filling state, when the dishwasher contains dirty dishes:

If you haven’t read this type of system diagram before, it should be quite intuitive: the arrows represent flow of materials, and the box represents containers that accumulate materials. So the houshold has some dishes, and they use them, at which point they either end up on the counter or in the dishwasher. The ones that end up on the counter eventually flow to the dishwasher. Once the dishwasher has run, the dishes flow back into the household.
Significant Thresholds
What I want to look at here is what happens to the system behaviour as we adjust the black arrow, i.e. the effort we spend on transporting materials through this link of the system. Let’s start analysis just after the dishwasher has run, i.e. the system is in the emptying state.
Resting Behaviour
If we invest no effort in emptying the dishwasher, we get the resting behaviour of the system: dishes accumulate on the counter. Assuming the household has access to infinite clean dishes, there will eventually be an infinite mountain of dishes on the counter. This is a bad place to be in.
Zero To One
The first significant threshold might be clear from above: it happens when we take the first clean dish out of the dishwasher.
This does not change anything about the system behaviour: we will still eventually end up with an infinite mountain of dishes on the counter, because we are pitching a one-time action against a rate of flow. The rate of flow will almost always win out in the long run. You often see people celebrating one-time changes, even though the rates of flow have not changed and it’s only a matter of time before things are as bad as they were before; people underestimate the power of ongoing flow.3 Typical example is a bug bankruptcy where one closes all bug reports older than some date. This is a one-time change, and eventually the flow of new bugs will catch up and you’re back at the same position again. If we want permanent change, we need to do something about the flows of bugs, not apply a one-time fix to the current count.,4 Another example is the “we need to rewrite this entire subsystem to improve it!” Generally, no. A steady stream of incremental improvements, over time, beats out the big-bang effort. Especially when there’s a limited budget.
If the first clean dish does not change the dynamics of the system, then why is it important? That has more to do with human reasons: it indicates we have gone from not caring about the problem to at least trying to do something about it, even if it’s insufficient.
Emptied Dishwasher
This is the point I really wanted to get to. If there’s only one thing you remember from this article, make it this one. The Threshold is passed when we have managed to transfer enough dishes out of the dishwasher that it is now empty. When that happens, the systems transitions into the filling state, at which point our household stops building on the counter mountain.
The reason this is so significant is that we have moved from a condition in which we had time as our enemy (waiting grows the counter mountain) into a condition where time is neutral to us.
If you have a system like the dishwasher one, and you have limited budget to improve the flows under your control, it pays off to spend a lot of that budget up front to get to the point where the system transitions into a state where time is no longer your enemy.
Once we’ve transitioned into the filling state, we can work as slowly as we want on moving dishes from the counter to the dishwasher, assured in the knowledge that the counter mountain is no longer growing, meaning it will eventually disappear with even the smallest amount of ongoing work.
If our household also helps out transporting dishes from the counter into the dishwasher once it’s emptied, then it becomes even more powerful to get to this state. In that case, time is actually our friend: once we get the dishwasher emptied, we can sit back and relax and do nothing else, and trust that eventually the counter mountain will work itself off.5 The example from software development I have here is when customers resist an improvement. Even if you can’t spend the money to convince customers to accept the improvement, it is worth spending whatever budget you have to get the improvement to become the default for new customers as soon as possible. Once the improvement is the default for new customers, time is on your side: natural customer churn will ensure that eventually, the improvement is in place across the board.
Another way to look at this is that when we get the dishwasher to empty, we shouldn’t think of that as achieving some goal for the current count of dishes in the dishwasher. We have done something much more fundamental: we have rearranged the flows of material in the system!
Matching Rates
Matching rates is not a significant threshold in the dishwasher system we have seen so far. But let’s imagine for a moment that we have a lazy household, and the filling state looks like this6 In other words, our household doesn’t put dirty dishes in the dishwasher even when it contains dirty dishes, they continue to put them on the counter, for us to transfer into the dishwasher.:
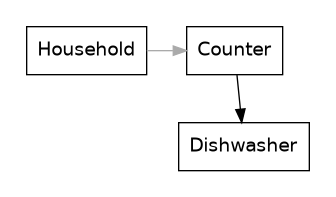
In this system, nothing significant happens when we have emptied the dishwasher: the counter mountain will still keep growing. In fact, there’s no magical threshold like in the previous system. The closest we get in this new system is the threshold that we pass when we start to transfer dishes from the counter to the dishwasher at the same rate as our household produces dirty dishes on the counter. That is the point at which the mountain on the counter stops growing.7 This is similar to the bug bankruptcy situation mentioned earlier. People often focus too much on the current counts, and not the flows. You might look at how much work you have to do and think that you need to employ more people. But the alternative interpretation is that you’re promising to do too much work, and that’s the rate that needs to be reduced. Any time there’s an imbalance, people tend to forget there are two things that need to be balanced, and focus on just one of the sides of the scale.
This might sound like we have time on our side, but it’s not quite the same thing because if we stop working at this high pace, the counter mountain will start growing again. For it to truly count as having time on our side, we should be able to stop working without making the situation worse.
Not Significant
Perhaps curiously missing from this list is the point when we have emptied the counter. The reason it’s not on there is that there’s not much that fundamentally changes about any of the systems we’ve discussed when the counter is empty. The time-dependent behaviour of the systems remains almost exactly the same.
This echoes the general sentiment in this article: the current counts of material don’t matter as much as the flows of material. This applies broadly to any systems.