Incident Inference From Symptoms
An acquaintance was feeling what could have been early symptoms of illness, but wanted to run a 10k race later that day. They approached me because they sensed there was a statistical problem in there: how should they react to symptoms getting worse during the race? Is that a sign to quit, or is it likely to be a false positive?
The conclusion was surprising and interesting, so for this article, I’ve recast the problem in terms of site reliability engineering, to be more relevant to my audience. In other words: if we see light symptoms of an incident during a high-traffic event, should we view that as an invitation to drop dinner and start investigating the problem, or should we count it as a false positive?
Appropriate restlessness during normal days
We have a web service that is about to be hit with lots of traffic during a large event. We’re worried about a serious downtime-causing incident, so we’ll keep our eyes on response times and be vigilant for the presence of symptoms.
We have learned during normal, non-event days that sometimes we see light symptoms even in the absence of an incident. We have learned to ignore these during normal days, because otherwise we’d burn ourselves out chasing false alarms. The probability of seeing light symtoms (\(S\)) during a normal, non-event day (\(\neg E\)) even in the absence of an incident (\(\neg I\)) is around 5 %, which we write mathematically as
\[P(S \mid \neg I, \neg E) = 0.05\]
The reason we don’t need to panic at light symptoms is that incidents are rare enough compared to this rate of false positives that we mostly don’t make a mistake by waiting for more serious symptoms to present themselves before dropping our dinner to attend to the problem.
Mathematically, we write the probability of an incident, given symptoms on a normal day, as
\[P(I \mid S, \neg E)\]
For the sake of argument, we don’t know exactly what this number is, but it is acceptably low.
Measuring risk of exposure with the odds ratio
With the event around the corner, we want to know how we should react to seeing light symptoms during the event. Should we drop dinner at the first indication of trouble, or stay cool? It might make sense to be extra jittery, because the high-traffic event does significantly increase the risk of an incident (maybe by 4×).
Another way to phrase this question is
How much worse is the risk of an incident during an event, provided that we see light symptoms?
This measure of “how much bigger is the risk” is often given as an odds ratio. It can be evaluated as the fraction of two probabilies, one with the risk factor present, and the other with it absent. In our case:
\[\mathrm{OR} = \frac{P(I \mid S, E)}{P(I \mid S, \neg E)}\]
If this odds ratio is sufficiently larger than 1.0, it indicates we should drop our dinner when we see light symptoms during the event, even if we would normally ignore such light symptoms. Let’s say we’ll change our policy of playing it cool during the event if this odds ratio is greater than 5×.1 The actual threshold is a function of the cost of an incident during the event compared to a normal day, but to avoid mixing risk management into this and get past this decision point let’s just go with a round number of 5× for the example.
Simplifying expressions
Through the chain rule of probability, we can rewrite
\[P(I \mid S, E) = \frac{P(I, S, E)}{P(S, E)}\]
We’ll do this for both numerator and denominator in the odds ratio, which turns it into
\[\mathrm{OR} = \frac{P(I, S, E)\; P(S, \neg E)}{P(I, S, \neg E)\; P(S, E)}\]
It is not obvious yet how this is useful, but we will get there shortly.
We can model the influences of the conditions (\(S\), \(I\), and \(E\)) on each other as a Bayesian network. We have these conditions affecting each other:
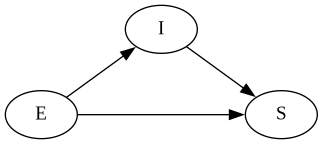
The arrow between \(E\) and \(I\) indicates that an event influences the probability of an incident. Both an incident and the event itself influences the presence of symptoms, which is why the \(S\) node has both \(E\) and \(I\) as parents.
The joint probability distribution of this network2 Here the lower-case letters are variables, i.e. we are in principle enumerating all possible \(2^3\) combinations of conditions and assigning each a probability. is \(P(e, i, s)\). Since this is a Bayesian network, we can decompose this full joint probability3 The way to find this decomposition is to start with the terminal nodes (those that don’t have children) and write out their probabilities conditional on their parents. Then we do the same for their parents, and so on. At some point we reach root nodes (with no parents) and we write out their marginal (unconditional) probabilities. into
\[P(e, i, s) = P(e)\; P( i \mid e)\; P(s \mid i, e)\]
With this, we can expand the full joint probabilities in the odds ratio:
\[\mathrm{OR} = \frac{ P(E)\; P( I \mid E)\; P(S \mid I, E)\; P(S, \neg E) }{P(\neg E)\; P( I \mid \neg E)\; P(S \mid I, \neg E)\; P(S, E) }\]
And then we expand the rightmost two joint probabilities also:
\[\mathrm{OR} = \frac{ P(E)\; P( I \mid E)\; P(S \mid I, E)\; P(S \mid \neg E)\; P(\neg E) }{P(\neg E)\; P( I \mid \neg E)\; P(S \mid I, \neg E)\; P(S \mid E)\; P(E) }\]
And this! Finally! Causes some useful cancelling, namely \(P(E)\) and \(P(\neg E)\) disappearing from the expression, yielding
\[\mathrm{OR} = \frac{ P( I \mid E)\; P(S \mid I, E)\; P(S \mid \neg E) }{P( I \mid \neg E)\; P(S \mid I, \neg E)\; P(S \mid E) }\]
We were actually looking for this cancellation all along, because the probability of an event should not affect the odds ratio we are seeking. We already know there will be an event, and we want to compare this to a situation where we know there is no event. The probability of an event is entirely irrelevant for that question. Seeing them cancel out is a sign we did something right.4 And indeed in my failed attempts at solving this, I knew I had failed specifically because because P(E) didn’t disappear.
Estimating conditional probabilities
At this point we have only conditional probabilities that are fairly easy to estimate with some operational experience of the system. For example, we may judge, that an incident is 4= as likely during an event as during a normal day:
\[\frac{P(I \mid E)}{P(I \mid \neg E)} = 4\]
Also, we might judge that we are a little more likely to notice the early symptoms of an incident during a high-traffic event, compared to a normal day:
\[\frac{P(S \mid I, E)}{P(S \mid I, \neg E)} = 1.1\]
The rightmost conditional probabilities
\[\frac{P(S \mid \neg E)}{P(S \mid E)}\]
aren’t as easy to estimate, because the effect of the event on seeing symptoms with or without an event is mediated by the presence or absence of an incident. We can make the estimation easier by extending the conversation:
\[P(S \mid E) = \sum_i P(S \mid I=i, E) P(I=i \mid E)\]
and estimating for the incident and no-incident cases separately. We might guess that
\[P(S \mid E) \approx 0.95 \times 0.04 + 0.4 \times 0.96 \approx 0.42\]
and
\[P(S \mid \neg E) = 0.85 \times 0.01 + 0.05 \times 0.99 \approx 0.06\]
Are these the correct probabilities?
¯\_(ツ)_/¯
At the level of approximation we are doing this, it is more important that we are not overconfident than that we are correct, whatever correct would mean.5 I’d argue, in the spirit of de Finetti and Savage, that any assignment of probabilities is as correct as any other, as long as its self-coherent.
Putting it together again
This means we have the following final estimation of the odds ratio:
\[\mathrm{OR} \approx 4 \times 1.1 \times \frac{0.06}{0.42} \approx 0.6\]
An odds ratio of 0.6 means that if we see light symptoms of an incident during an event, we should be less concerned than if we saw them outside of an event. This took me and my acquaintance by surprise, but in hindsight it makes sense.
Yes, the event increases the risk of an incident fourfold, and it somewhat increases the chance that meaningful symptoms are produced – but it also increases the probability of seeing spurious symptoms by so much that symptoms become a weaker signal than they were during a normal day.
We should continue to play it cool during the event. And my acquaintance did run the 10k, did feel symptoms, assumed they were spurious as they would any other day, and was fine afterwards.