Markov Chains for Queueing Systems
Table of Contents
I’m finally taking the time to learn queueing theory more properly, and one of the exercises in the book I’m reading1 Performance Modeling and Design of Computer Systems; Harchol-Balter; Cambridge University Press; 2013. really got me with how simple it was, yet how much it revealed about how to analyse some queueing systems without simulating them.
Here’s the setup:
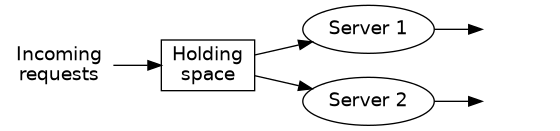
- This is a system with two servers, and each can only handle one request at a time.
- If any server is idle when a request comes in, it immediately begins processing that request.
- If both servers are busy when a request comes in, the request gets placed in the holding space and waits for as long as it needs to until a server becomes free again.
- If another request comes in when the holding space is occupied, the incoming request is rejected. (I.e. the system can contain at most three requests at a time.)2 You might complain the size limit of 3 requests is unrealistic and makes the exercise pointless, but you’d be wrong. The analysis is exactly the same as for a bigger system, but with this limited setup, we can hold the entire problem in our heads at the same time. Later, we’ll talk about ways to change the scale of the system.
Now we want to know some things about this system:
- What fraction of the time is the system completely idle? (I.e. have we paid too much for servers that are mainly idle?)
- When two servers are busy, how often does the holding space need to be used?
- How many requests will we reject because the system is full?
- Is this system performant? What’s the throughput and average response time like?
These are the types of questions I would normally use performance testing on the already-built system to answer. (In other words, I would be able to answer them, but only too late – once the system is built.) Under some (more or less mild) assumptions, we can actually derive the answers analytically, without building or running anything.
Further, we may want to suggest design changes to this system. Should we get faster servers? Or cheaper, slower servers? Or more servers? Or fewer servers? Or a larger holding space? These are all questions we can answer analytically too.
This is a very fast, iterative process that lets us search the design space for the right solution given the constraints we have. This is the engineering part of oftware engineering.
Specification of System
We will start with some assumptions on the behaviour of the requests. We will say that the time between each incoming request is exponentially distributed with rate \(\lambda\). We also think that the time it takes to process each request is distributed exponentially, but with rate \(\mu\).3 These Greek letters are conventional for arrival rate and processing rate in queueing theory.,4 You might be concerned that we are just assuming theoretical distributions for important quantities of analysis. You are right to be concerned. The assumption about the arrival distribution turns out is theoretically very important, and practically usually workable. The assumption about processing time is the one you have to be particularly careful about. However, let’s assume we’ve verified that in the system we have here, it’s close enough to make practical decisions. Recall that the purpose of models is not to be right, but to be useful.
To help with intuition, let’s say that \(\lambda = 75\). In other words, this system receives on average 75 requests per second. We also have \(\mu = 110\), meaning our servers can process requests at a rate of 110 requests per second on average.
Intuition check 1: You might notice that the processing rate is faster than the request rate. Could we use only one server and avoid having to pay for two?
Intuition check 2: What would happen if the servers only could handle 50 requests per second?
Markov Chain Model
The system has four states, each corresponding to the number of requests in the system. Each state transitions to the next with rate \(\lambda\), except in \(s_3\) (where there are three requests in the system and the holding space is occupied), because at that point no additional requests are accepted.
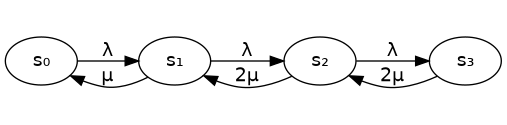
However, requests are also processed by the servers, meaning that in state \(s_1\) (one request is processed by one server), the system transitions back to \(s_0\) (completely idle) at a rate of \(\mu\). Once there are two requests being processed (in parallel, because there are two servers), the transition back to lower states happens twice as fast – at a rate of \(2\mu\).
Easy Question
Holding Space Usage
This is the easiest of the questions to answer, because it asks for the probability of needing the holding space provided that both sevrers are busy. That condition means we can derive the probability just from the transition rates, without knowing how often both servers are busy.
What we’re essentially asking here is “if we find ourselves in a situation where both servers are busy, what is the probability that another request arrives before one of the servers are finished with the requests they are processing?”
Intuition check 3: Recall that we get 75 requests/second into the system on average, and our servers can process them at an average rate of 110 requests/second. What do you think is the probability that another request comes in before one of the servers is finished? What does your gut say?
Let’s find out. The state in the Markov chain where both servers are busy and the holding space is free is \(s_2\). This can transition either up to \(s_3\) if another request arrives first, or back down to \(s_1\), if one of the servers finish processing a request first. The total rate of transitions out of \(s_2\) is then \(\lambda + 2\mu\). The probability that another request arrives first is, thanks to the exponential distribution,
\[P_{2,3} = \frac{\lambda}{\lambda + 2\mu}\]
In other words, if we’re talking about exponentially distributed times between events, the probability that a particular event happens first is just the rate of that event divided by the total rate of all events that can happen.
Given our specific system specifications, we have
\[P_{2,3} = \frac{75}{75 + 2 \cdot 110} \approx 25 \%\]
Thus, when the two servers are busy, it’s most likely one of them will be free before the next request arrives, but one in four times, the next request ends up in the holding space instead.
Interlude: State Probabilities
The remaining questions require us to know how often each state is visited, i.e. how often the system is idle, how often there is one request being processed, how often both servers are busy at the same time, and how often the holding space is used.
Since we have concrete numbers for \(\lambda\) and \(\mu\), we could of course just simulate this on the computer. However, imagine that we haven’t designed the system yet, and we want to find the appropriate tradeoffs between \(\lambda\), \(\mu\), number of servers, etc. Then it’s useful to solve the problem analytically to get formulas for the quantities.
If you’re not theoretically inclined, feel free to skip this section at your own peril. Do scroll to the bottom of the section though, and make note of the final equations for \(\pi_0\), \(\pi_1\), \(\pi_2\), and \(\pi_3\). We will use them later.
There are various ways to figure out the state probabilities analytically. One of my favourite ways – when possible – is the time reversibility equations. As you can see in the system diagram, the only way to get from a state to any other is to pass through all the states in between. The consequence of this is that the total rate of transitions out of a state is equal to the total rate of transitions into a state. We can set up equations to represent this.
In these equations, we write \(\pi_0\) to indicate the probability of being in state \(s_0\), and so on. First off, \(\pi_0\) is easy because there’s only one transition out of \(s_0\) (at rate \(\lambda\)) and one transition into it (from \(s_1\) with rate \(\mu\).)
\[\pi_0 \lambda = \pi_1 \mu\]
Then \(\pi_1\) is a little more complicated, because there are two transitions out of and in to \(s_1\).
\[\pi_1 (\lambda + \mu) = \pi_0 \lambda + \pi_2 2\mu\]
The rest follow a similar pattern.
\[\pi_2 (\lambda + 2\mu) = \pi_1 \lambda + \pi_3 2\mu\]
\[\pi_3 2\mu = \pi_2 \lambda\].
If we rearrange things5 This takes a bit of algebraic manipulation, work through it if you’re interested., we get the following:
\[\pi_1 = \pi_0 \frac{\lambda}{\mu}\]
\[\pi_2 = \pi_0 \left(\frac{\lambda}{\mu}\right)^2 \frac{1}{2}\]
\[\pi_3 = \pi_0 \left(\frac{\lambda}{\mu}\right)^3 \frac{1}{4}\]
At this point, it’s useful to provide another definition from queueing theory. The quantity \(R = \lambda / \mu\) is useful to make equations like these simpler.6 What does \(R\) mean? One way to think of it is as the average number of requests being processed simultaneously. With that, we have
\[\pi_1 = \pi_0 R\]
\[\pi_2 = \pi_0 \frac{R^2}{2}\]
\[\pi_3 = \pi_0 \frac{R^3}{4}\]
Now we only need to know \(\pi_0\) to be able to compute all the other probabilities. What we do know is that we can only be in one state at a time, and there’s a 100 % probability that we is in some state. Mathematically, we write
\[1 = \pi_0 + \pi_1 + \pi_2 + \pi_3\]
into which we insert the definitions above, and rearrange it to give us
\[\pi_0 = \left(1 + R + \frac{R^2}{2} + \frac{R^3}{4}\right)^{-1}\]
Now, given \(R\) (or, by extension, \(\lambda\) and \(\mu\)) we can actually figure out the probabilities of being in any state. That’s quite amazing! We can know how likely various levels of load on our queueing system is, just based on the rates involved.
It’s very convenient, by the way, that this result depends only on \(R\). If we imagine selling this system to various customers, we would only have to pick a proper \(R\) in the design space, and then vary how powerful the servers are (i.e. \(\mu\)) based on each specific customer’s requirements for the request rate \(\lambda\).
Let’s move on to the questions again.
Difficult Questions
System Idle Time
One of the things we wanted to know was how often the system is idle. Basically, how much of the hours of the day are we paying for expensive servers doing absolutely nothing? This is a measure of how much we have over-sized the system.
Intuition check 4: Recall that the request rate into the system is 75 requests/second, and our servers can process on average 110 requests/second. What percentage of the time do you think both our servers are completely idle? Do you have any intuitive sense for this?
For the actual answer, we can go back to the definition of \(\pi_0\) from the last question, because that is the probability that the Markov chain is in the “completely idle” state. We plug in \(\lambda = 75\) and \(\mu = 110\) and get \(R=0.68\), which then goes into
\[\pi_0 = \left(1 + 0.68 + \frac{0.68^2}{2} + \frac{0.68^3}{4}\right)^{-1} \approx 0.5\]
We find that roughly half the time, our system stands completely idle! Whether or not this is acceptable might depend on the performance metrics we’ll compute next: the request rejection rate and metrics like response time and throughput.
How does this vary with \(R\)? Well, quite simply:
In other words, the more requests your servers have to answer simultaneously, the less likely they are to be idle.7 Someone who has dabbled in queueing theory might be confused that there is still some probability the servers are idle when R is greater than 2. This is because this is a rejecting system. Rejecting a bunch of requests during a burst tends to leave the system more breathing room afterward. It’s never stuck catching up on a long backlog of requests.
Request Rejection Rate
How often are requests rejected? This is asking “how often is the system in state \(s_3\) and what’s the rate of incoming additional requests then, that have to be rejected?”
Intuition check 5: Again, we have 75 requests/second incoming on average, and an average processing rate of 110 requests/second for each server. How often do you think requests would be rejected, if you went with your gut feeling?
We can work out the fraction of the time the server is in state \(s_3\), which is
\[\pi_3 = \frac{R^3}{4} \pi_0\]
Then we need to multiply this with \(\lambda\) to get the total rate of requests received in this state (all requests received in that state will be rejected). Let’s call the rate of rejected requests \(v_r\). In our system (see previous question about \(\pi_0\)), this will be
\[v_r = \pi_3 \lambda = \frac{0.68^3}{4} \cdot 0.5 \cdot 75 \approx 3\]
In other words, we will reject 3 requests per second, or 4 % of our workload. This might not be considered great, so we’ll get back to that!
System Performance: Throughput
Let’s look at throughput (denoted \(X\)). In a non-rejecting queue, this is easy:
\[X = \lambda\]
This is because every request is served eventually, and that some take longer and some go faster averages out over time. It’s a common mistake to think that the throughput will be equal to the maximum processing rate \(\mu\), but note that the maximum processing rate is never the rate we operate at in production – that would be insane!8 It leads to an infinite queue, thus rendering the system practically unavailable, even if it’s processing things as fast as it can.
We know that our system rejects \(v_r\) requests of the \(\lambda\) received. So the throughput is, quite naturally,
\[X = \lambda - v_r\]
Or, for our current system specifications,
\[X = 75 - 3 = 72\]
Thus, the throughput is 72 requests per second.
System Performance: Response Time
Response time is in many cases one of the most important system performance metrics.
Intuition check: What do you think is the response time of our system where each server can handle 110 requests per second?
We can calculate the average response time through Little’s law, which says that average response time \(E(T)\) is given by the average number of requests in the system \(E(N)\), divided by the throughput (X).
Stated mathematically, then, Little’s law says that
\[E(T) = \frac{E(N)}{X}\]
This should be quite intuitive: if you arrive at a bank and there are 6 people ahead of you in line, and the counter seems to be able to handle 12 people per hour, then you know you’ll be there for half an hour.
We know the throughput. How do we figure out the average number of requests in the system? We know the probabilities of each state (\(\pi_0\), \(\pi_1\), etc.) and how many requests are in the system for each of those states (0, 1, etc.) We can compute that weighted average:
\[E(N) = 0\pi_0 + 1\pi_1 + 2\pi_2 + 3\pi_3 =\]
\[= 0\pi_0 + 1\pi_0 R + 2\pi_0 \frac{R^2}{2} + 3\pi_0 \frac{R^3}{4}\]
Using numbers from our system, we have:
\[ E(N) = 0.5 \left(0 + 0.68 + 2 \frac{0.68^2}{2} + 3 \frac{0.68^3}{4}\right) \approx 0.69\]
So we have on average 0.69 requests in the system. This makes the response time
\[ E(T) = \frac{0.69}{72} \approx 0.0096\]
That’s in seconds, so 9.6 milliseconds.9 Note that if we used the arrival rate \(\lambda\) instead of the throughput \(X\) for this, it would look like the response time was faster. That confused me at first: why would we get a slower response time by rejecting requests? But that’s reading the causation the wrong way around: we are forced to drop requests because the response time is too slow not to! That’s about as fast as we can expect, given that the maximum theoretical response time our servers can offer is
\[ T_\mathrm{max} = \frac{1}{110} \approx 0.0091\]
This makes sense: our system stands idle most of the time, so whenever a request comes in, it’s likely it will get the full attention of one of the servers. Only rarely does it have to hang out in the holding space for a short while.
System Changes
The above analysis has yielded these results:
| Idle time | Rejected | Throughput | Response time |
|---|---|---|---|
| 50 % | 3 req/s | 72 req/s | 9.6 ms |
We can look into some potential improvements, and see how they affect things. Please note that for all of the following, we have run zero load tests – it’s all done on paper by solving the equations above.
Slower, Cheaper Servers
We know that our servers are idle a lot, so maybe we should work with slower servers. We think that 110 requests/second is too much, and the next step down is a server type that does 60 requests/second. If we evaluate the equations at that point instead, we get the following comparison
| Servers | Idle time | Rejected | Throughput | Response time |
|---|---|---|---|---|
| 2 @ 110 req/s | 50 % | 3 req/s | 72 req/s | 9.6 ms |
| 2 @ 60 req/s | 28 % | 10 req/s | 65 req/s | 18.8 ms |
This doesn’t look very good, though. Two of the 60 requests/second servers are very cheap, but they also don’t perform very well.
More Servers
What if we get three servers of the slower kind, instead of just two? Or maybe even four? Four servers that can do 60 requests/second ought to be a little bit better than two servers that do 110 requests/second – and it’s still cheaper.
| Servers | Idle time | Rejected | Throughput | Response time |
|---|---|---|---|---|
| 2 @ 110 req/s | 50 % | 3 req/s | 72 req/s | 9.6 ms |
| 3 @ 60 req/s | 29 % | 3 req/s | 72 req/s | 17.2 ms |
| 4 @ 60 req/s | 29 % | 0.7 req/s | 74 req/s | 16.8 ms |
Note that it takes three of the slower servers to match the rejection rate of two of the faster ones – but the response time is much worse! Getting four servers improves the rejection rate, but doesn’t do much for response time.
We like the idea of three slower servers, but our customer complains about the rejection rate.
Bigger Holding Space
One obvious thing to do to improve the rejection rate is to make the holding space bigger, so more requests can wait for a free server.
If we keep the three slower servers and adjust the size of the holding space, we have the following results:
| Holding space | Idle time | Rejected | Throughput | Response time |
|---|---|---|---|---|
| 0 | 30 % | 7 req/s | 68 req/s | 16.7 ms |
| 1 | 29 % | 3 req/s | 72 req/s | 17.2 ms |
| 2 | 28 % | 1 req/s | 74 req/s | 17.6 ms |
| 4 | 28 % | 0.2 req/s | 75 req/s | 18.0 ms |
| 8 | 28 % | 0.006 req/s | 75 req/s | 18.1 ms |
Some, perhaps obvious, observations:
- Adding more queueing does not actually improve the performance of our system. What it does is turn immediate rejections into slower responses – as can be witnessed by the increasing response time as queueing spaces are added.
- A longer queue to work on means less idle time for the servers – but this isn’t necessarily a good thing: the servers might now be working on requests where the results are no longer relevant for the customer.
One Fat Server
It turns out that response time is very important for our customer. They work in a high-speed industry, and a response that comes a few milliseconds late might as well never have arrived. In particular, they have now clarified that they need an average response time10 If you’ve done high-speed stuff, you know that nobody in their right mind would measure response times by the average. Analysing the full distribution of performance from a queueing system will have to be a separate article, though, so just play along here, please. of less than 10 ms, and a request rejection rate of less than 1 request/second. We cannot provide that response time with 60 request/second servers, because the fastest response time they can provide is \(1/60 = 16.7\) ms.
There’s also no queue length that gives the two 110 request/second servers the correct combination of response time and rejection rate: if the queue is long enough to guarantee rejection rate less than 1 per second, the response time is just over 10 ms, and vice versa.
So we try instead one, fat, 195 requests/second server.
| Servers | Idle time | Rejected | Throughput | Response time |
|---|---|---|---|---|
| 2 @ 110 req/s | 50 % | 3 req/s | 72 req/s | 9.6 ms |
| 1 @ 195 req/s | 65 % | 7 req/s | 68 req/s | 6.6 ms |
With this, the response time looks great, but everything else seems terrible. However, we try increasing the holding space to size four for the fat server:
| Holding space | Idle time | Rejected | Throughput | Response time |
|---|---|---|---|---|
| 1 | 65 % | 7 req/s | 68 req/s | 6.6 ms |
| 4 | 62 % | 0.4 req/s | 75 req/s | 8.1 ms |
We are there!
This beastly server stands idle a lot of the time, but that’s what it takes to have fast response times. This goes back to Little’s law, which makes it a very general rule: in order to guarantee fast response, you have to have few things going on.
There’s anothing thing worth noting: we saw before that queues don’t improve performance. However, if performance is good enough to begin with, we can afford longer queues to soak up variability in the work demanded of our servers. But only if we have good performance to begin with.
Yet one more observation: a queue on a performant system doesn’t have to be very long to soak up a lot of variability. It’s when you have a slow system that the queue needs to be really long to avoid rejecting things. But then again, you’re not serving them any faster, you’re just turning rejection into waiting.