Probability-Generating Functions
I have long struggled with understanding what probability-generating functions are and how to intuit them. There were two pieces of the puzzle missing for me, and we’ll go through both in this article.
There’s no real reason for anyone other than me to care about this, but if you’ve ever heard the term pgf or characteristic function and you’re curious what it’s about, hop on for the ride!
Sequences of numbers without vectors
Imagine you are holding five regular playing cards in your hand. Maybe your hand is QQA97, i.e. a pair of queens, an ace, a nine, and a seven. We’re playing some sort of weird poker variant where I get to blindly draw one of your cards. We’re curious about the probability distribution of the outcome of that draw.
In words, most cards (e.g. 2, 4, 8, J and others) have a probability of zero of being drawn from your hand (because they are not in your hand.) Some cards (ace, seven, nine) have a 20 % probability of being drawn, and then there’s a 40 % probability that a queen is drawn, since you have two of them.
Numerically, we might today phrase this as a vector with these values (taking ace to be low):
\[\left[1/5,\;0,\;0,\;0,\;0,\;0,\;1/5,\;0,\;1/5,\;0,\;0,\;2/5,\;0\right]\]
When de Moivre invented much of modern probability in the mid-1700s, he didn’t have vectors! Vectors are an 1800s invention.
Sure, he could write sequences of numbers down, but at the time they didn’t have a systematic way of dealing with those sequences as a single unit. They were just that: sequences of separate numbers. However, there was another way for him to turn many numbers into a single object: by embedding them as coefficients in a polynomial function.
Polynomials encoding sequences are generating functions
If we want to encode the vector \(\left[6, 2, 8, 4\right]\) in a single expression and we cannot use vectors, we can create a function
\[f(x) = 6 + 2x + 8x^2 + 4x^3\]
and this function now contains all those numbers. One might imagine that this function would be reducible into some simpler expression by combining terms and multiplying out \(x\)s, but thanks to the increasing powers of \(x\), it is not. Regardless of how this function is rearranged, we will still be able to arrange it back into this shape. We can extract any number in the sequence from this function with some calculus if we want to1 If we want to extract, say, the third number (in this case 8), we will need to take the second derivative (to isolate that number as a constant), evaluate the function at zero (to get the constant out) and then divide by two (to remove excess coefficient that came from the derivative action.) More generally, number \(n\) is found through \(f^{(n-1)}(0)/(n-1)!\)., emphasising how the polynomial and the vector really are, in some sense, carrying the same information.
We might be curious about what the \(x\) represents. Like, what are typical values we might plug in for \(x\)? The answer is nothing. We generally don’t evaluate this function with any \(x\) at all. The function, and \(x\), exists only to create a particular structure into which we can store coefficients for later manipulation. it is not intended for anything meaningful to come out if we replace \(x\) with some specific value we might think of.2 That said, we have already seen in an earlier sidenote that the value x=0 is special in that it allows us to extract the constant, which combined with differentiation lets us extract any coefficient. But although there are some \(x\) that result in something meaningful, we shouldn’t think all \(x\) do.
What we just did was turn a vector into a polynomial. Today, the inverse operation is probably more common in that we take the coefficients of a long polynomial and plug them into a vector to e.g. find roots with linear algebra. But back in the time of de Moivre, polynomials were all they had, and so when they needed to work with an entire sequence as a single object, they chucked the sequence in as coefficients of a polynomial function. The polynomial \(f(x)\) is then known as a generating function of the sequence, because we can (through calculus) generate each value of the sequence from the function \(f(x)\).
Probability-generating functions
The probability distribution of a draw from your hand, you know, that vector
\[\left[1/5,\;0,\;0,\;0,\;0,\;0,\;1/5,\;0,\;1/5,\;0,\;0,\;2/5,\;0\right]\]
might then be represented by the polynomial (generating) function3 Taking the convention that aces can be represented numerically as 1, and queens as 12.
\[G(t) = \frac{1}{5}t^1 + \frac{1}{5}t^7 + \frac{1}{5}t^9 + \frac{2}{5}t^{12}\]
In this case, the numbers in the sequence – and the coefficients of the generating function – are probabilities. When the coefficients of a generating function are probabiilties, we call that function a probability-generating function.
Coin flips and their probability-generating functions
We have some other examples of probability-generating functions. For example, a fair coin flip has a probability-generating function
\[G(t) = 0.5t^0 + 0.5t^1\]
because outcome 0 (tails) has probability 50 % and outcome 1 (heads) has probability 50 %.
If the coin is not fair, but has bias \(p\), then the probability-generating function is
\[G(t) = (1-p)t^0 + pt^1\]
This is often written more compactly as4 Using the fact that for any \(t\), we can say that \(t^0 = 1\), and we usually write \(t^1\) as just \(t\).
\[G(t) = (1-p) + pt\]
The geometric distribution represents how many tails we have to see until the first heads. In the case of a fair coin, we expect to get heads very soon, but when the probability \(p\) of heads is low, we may have to toss for a very long time. We can think systematically to guess the sequence of probabilities for the geometric distribution5 With probability \(p\) we get heads on the first toss. In that case, we will have zero tails, and this will be the first value of the probability sequence. Failing to get heads on the first toss has probability \((1-p)\), which means if we get heads on the second toss, we will have seen an outcome with probability \((1-p)p\). Getting heads on the third toss has probability \((1-p)^2p\) because it requires two tails followed by heads. This goes on forever, but at this point we have caught on to the pattern: the first heads on the nth trial requires \(n-1\) tails followed by a heads, which has probability \((1-p)^{n-1}p\). and if we do, we end up with a sequence that in vector form looks like
\[\left[p,\;\;(1-p)p,\;\;(1-p)^2p,\;\;(1-p)^3p,\;\;\ldots\right]\]
As a generating function, that becomes
\[G(t) = pt^0 + (1-p)pt^1 + (1-p)^2pt^2 + (1-p)^3pt^3 + \ldots\]
It might seem troublesome that this function has an infinite number of terms, but that’s actually not a big deal. Not even to de Moivre! By the mid-1700s, although their proofs were not as rigorous as today’s, they had a decent grasp of polynomials of infinite degree.
In particular, we can define \(v = (1-p)t\) and rewrite this last probability-generating function of the geometric distribution as
\[G(t) = p \left( v^0 + v^1 + v^2 + \ldots \right)\]
and for sensible \(v\), this is equivalent to
\[G(t) = \frac{p}{1-v}\]
Substituting back, we get a very compact way to express the geometric distribution through its probability-generating function:
\[G(t) = \frac{p}{1 - (1 - p)t}\]
But remember that even though this function does not look anything like a series, it still encodes a series as a polynomial – it’s just been rearranged for compactness. We can still extract each individual probability from this through calculus.
That’s it. A probability-generating function is a way to encode a sequence of probabilities into a single object (a function) when one does not have access to the technology of vectors.
Except …
Properties of probability-generating functions
There are reasons to do this beyond “I wanted a sequence but I didn’t have vectors”, and it’s that the resulting probability-generating function has some convenient properties.
We have already seen that the probability-generating function has the following structure:
\[G(t) = p(0) t^0 + p(1) t^1 + p(2) t^2 + \ldots\]
In other words, each term is given by the probability of getting that value multiplied by \(t\) raised to that value.6 Where, we should be reminded, neither \(G(t)\) nor \(t\) really has a meaningful interpretation. The variable exists to force the function into a particular structure, it’s not meant to be evaluated at this point. Here are some more things we can do with probability-generating functions:
- A perhaps useless property is that if we evaluate \(G(1)\) we should get 1, because then we are but summing all coefficients, which are probabilities.
- One of the easiest meaningful properties is evaluating the first derivative at \(t=1\), i.e. taking the value of \(G' (1)\). When we do that, we get the expectation of the probability distribution!7 Feel free to verify this for yourself by differentiating some simple probability generating function. This surprised me at first, but seems sensical now.
- If we evaluate the curvature at the same point, i.e. \(G'' (1)\), we get the expectation of \(X(X-1)\), which in turn is a value that’s sort of related to the variance of the probability distribution.8 Look it up for more details. I’m not yet good enough to intuitively get why the curvature of the probability-generating would be related to variance, but I’d be happy to receive pointers here.
- If we multiply two probability-generating functions we get the convolution of the two distributions, i.e. the distribution of sums of draws from each original distribution. So if \(G\) is the probability-generating function of a die, then \(G(t)G(t) = G^2(t)\) is the probability-generating function of two dice thrown and then summed up.9 This is not, to modern eyes, as fascinating as it might seem. When we multiply two polynomials we multiply together all combinations of coefficients. We are effectively writing up a big 2D table of all possible outcomes of each draw, and multiplying their probabilities in each cell. Except we’re doing it in a way that is amenable to algebraic manipulation to someone who does not have vectors.
- Finally, if we have a randomly selected integer \(N\) with probability-generating function \(F\), and we want to know the distribution of a sum of \(N\) randomly selected \(X\), drawn with probability-generating function \(G\), we get the distribution of the sum from the probability-generating function \(F(G(t))\).
I believe the latter was one of the motivating cases for probability-generating functions, because this lets us solve the problem of the points, i.e. how to distribute the betting pot if we have to quit a game of dice early.
New here? I am a practicing software developer and I often write about things I learn in the area of probability and statistics. You should subscribe to receive weekly summaries of new articles by email. If you don't like it, you can unsubscribe any time.
Probability-generating function to characteristic function
We said before that we’re not meant to try to find a sensible value for the parameter \(t\). Despite this, some values are more sensible than others. In particular, we want \(|t| \le 1\) in order for an infinite-degree polynomial to converge on a value. So the values we tried with \(t=0\) and \(t=1\) are both more sensible than e.g. \(t=52\).
However! If we decide to go with \(t=e^{iu}\), then regardless of what \(u\) is, we will find \(t\) on the unit circle in the complex plane. This means we are guaranteed to have \(|t| = 1\), and all values \(u\) converge.10 Strictly speaking this is only true for real \(u\) I think. But that’s what a sensible person would think of anyway. When we use a parameter of the shape \(t=e^{iu}\), we write the function not as \(G(e^{iu})\) but more simply as \(\phi(u)\) and this is called the characteristic function.
Again, that’s it.11 Well, again, not quite, because there are all these useful properties of the characteristic function and it’s involved in a bunch of proofs and my analysis is way too weak to understand much of it.
Visualising the characteristic function
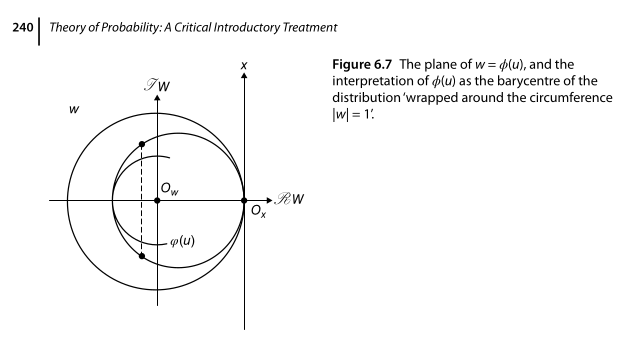
In Theory of Probability, de Finetti provides a nice visual of the transformation implied by the characteristic function. We will have a bunch of
\[\phi(u) = \ldots + p(-2) e^{-2iu} + p(-1) e^{-iu} + p(0) + p(1) e^{iu} + p(2) e^{2iu} + \ldots\]
If we focus on the case where \(u=1\), then each of the \(e^{iuX}\) represent a distance \(X\) traveled counter-clockwise (for \(X\) positive) or clockwise (for \(X\) negative) around the unit circle in the complex plane. Then when we multiply by \(p(X)\) we scale this point on the circle down closer to the origin based on its probability.
Visually, the sequence of \(p(X)e^{iuX}\) has the effect of wrapping the probability distribution of \(X\) around the unit circle in the complex plane into a kind of spiral. When we sum all these points together, we get the barycentre of that spiral, and that is indeed how we can intuit the value of \(\phi(u)\).
This also makes it clear that \(\phi(u)\) is real for symmetrical distributions, but complex in the general case.
I really wish I could animate this because it’s a great way to look at it, but instead, I give you the image we get from de Finetti:
The definitions are easy, the consequences are hard
I guess this leaves us at an unsatisfactory note: we have learned how simply these objects are defined, but we haven’t learned much about how to use them. Doing so takes higher level analysis than I’m capable of, so I’ll have to leave that article to someone else.