Word Embeddings in Perl: Baby Steps
Table of Contents
Continuing from our adventures into latent semantic analysis in Perl, I have been toying with neural networks, the ultimate goal being word2vec-style word embeddings.1 Again, not because I think the outcome will be practically useful – there are pre-trained word2vec models for that – but because I need an excuse to do something I’ve never done before: write a neural network.
Reading input–output pairs into a matrix
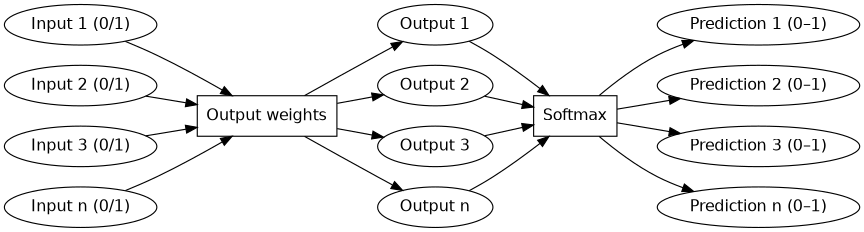
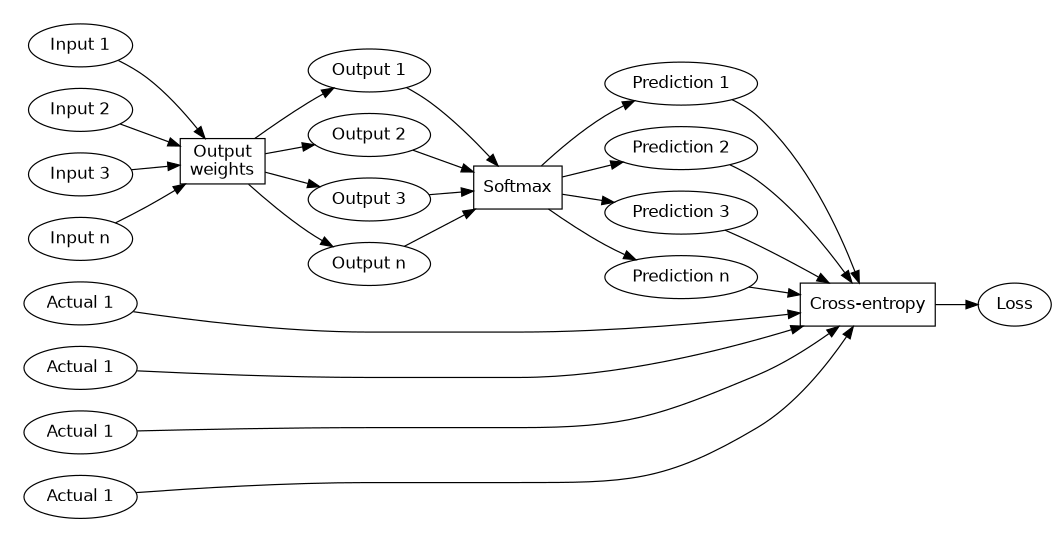
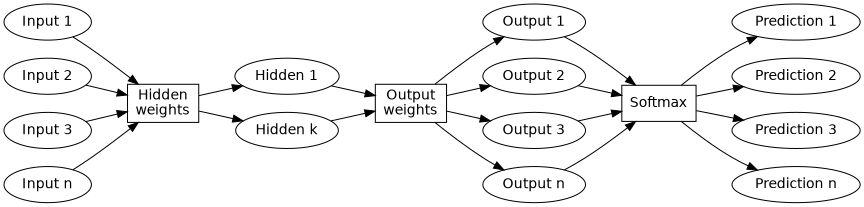
We can reuse some of the code from before to generate a list of significant terms, as well as generate a long list of pairs of such words that occur in close proximity to each other in the articles on this site. Then creating an input and an output matrix of one-hot coded words is not technically complicated:
# %important contains all significant words, so $vocab_width # is the total number of words in the vocabulary. my $vocab_width = scalar keys %important; # This limit exists to train on a subset of pairs only, because # the full set of pairs would take a long time to properly # train on. my $max_samples = 5000; my $inputs = zeroes $vocab_width, $max_samples; my $outputs = zeroes $vocab_width, $max_samples; open $fd, '< :encoding(UTF-8)', '30_pairs.txt'; $i = 0; while (defined ($_ = <$fd>) && $i < $max_samples) { chomp; my ($in, $out) = split ',', $_; # Get word indices of word pair. (my $ini, my $outi) = ($important{$in}, $important{$out}); # One-hot code this word pair. $inputs($ini, $i) .= 1; $outputs($outi, $i) .= 1; $i++; } $max_samples = $i if $i < $max_samples;
Example run
On a rather small vocabulary, these are a couple of examples for which the neural network predicts neighbouring words.
vocabulary size: 88 words
hidden layer size: 10 neurons
training data size: 4000 word pairs
training time run: 340000 iterations
forward: 35 seconds
evaluate: 30 seconds
backprop: 146 seconds
graddesc: 20 seconds
Top predicted for throughput:
idle (0.282926072456738)
queueing (0.203447311429027)
lambda (0.150047726808125)
approx (0.0677357006513723)
perl (0.0279980203695144)
Top predicted for parsers:
readp (0.320780649913162)
monad (0.253496002428353)
wind (0.201488443337817)
sensitivity (0.0437110736151976)
loops (0.040039343569064)
These predictions may not all seem entirely sensible out of context, but noting that they come from articles on this site, they seem rather sensible – I can point to the exact articles in which these pairs co-occur.
Problems and solutions
I have already encountered a few annoying problems during this process.
Garbage in, garbage out
For a while I had what I thought was a working neural network, except it kept predicting nonsense. I tried adjusting parameters, trying to train it for longer, reduced the vocabulary to just a few words, but nothing helped. After spending way too long trying to find a problem in the backpropagation, I realised I had given the network a nonsense vector for the input, rather than the one-hot vector corresponding to the word I thought I had asked it to predict.
This is a really good lesson. When code misbehaves, it’s almost always due to a bug in the code, rather than faulty input, so it’s easy to develop a heuristic to start debugging immediately. However, checking for faulty input is so much easier than debugging code that works, so it’s still a better first response to verify the input, on the off chance that this was one of those one-in-a-hundred times when the input really is the problem.
Slow code
We saw one optimisation in the section on backpropagation. I often profile code manually, by injecting counting logic in the code I suspect is slow, and then analyse the rates at which things happen.
For this code, I tried Perl’s NYTProf. It was a magical experience. It showed
not only which functions were slower than the rest, but also which statements
were slow. It even displayed which parts of each statement was slow!
Without that, it would have taken me much longer to figure out that the
innocent-looking statement $s_i * ($i_v - $s_j) was the main cause of slow
execution8 Blessing and curse of working with matrices. We get low-effort
vectorisation, but it’s also easy to accidentally work on huge data structures
without it being obvious in the code.. Optimising that statement away made
training go 20× faster.
Adjustment and evaluation
At this point there’s a neural network that seems to work for very small vocabularies. Adding more words makes it stop working. This is to be expected, if nothing else because more words means it needs to train for longer.9 Actually, we can also tweak the learning rate and the width of the hidden layer. This article is long enough already. Maybe we’ll take some time to explore that later.
The end goal is to run this network on at least 2000 words, ideally more. How much training will it need to work with that? But wait, let’s back up a little.
What does it even mean for it to work? I don’t know, to be honest. we can eyeball some predictions and say whether they look right or wrong, but that doesn’t scale. One idea is to select a few words randomly, and see how likely the top prediction candidates for those words are. If we look at a large enough number of candidates, their total probability should start out low but grow to near 100 % as training goes on. When it approaches 100 %, we might interpret that as the model having learned what those words are associated with.
To get a sense of when this happens, we can write a script that randomly walks
around in the parameter space10 In a throwback to the previous article, the
parameter space is actually the pair of numbers min_usages and min_idf from
before, which determines which words are considered significant. and for each
new position, it runs the neural network until it has learned the five random
words.
I was hoping to present a pretty graph, but the data is incredibly noisy.
Rather unsurprisingly, the number of training samples extracted from the articles on this site varies with the square of the size of the vocabulary of significant words.11 Whenever you have x things, you always have O(x²) pairs of things.
The speed at which the network converges might look like it, maybe, on very shaky data, decays exponentially in log-iterations12 That already sounds like bad news!. It starts out improving by almost 30 percentage points per log-iteration for the smallest data sets, but then as we get to 4000 sample pairs, it’s already down to 10 percentage points per log-iteration. At 15,000 sample pairs, it’s around 5 percentage points per log-iteration.
The vocabulary of 2000 words turns into 275753 pairs. According to the –
eyeballed – improvement model described above, these pairs would improve at a
rate of \(10^{-13}\) percentage points per log-iteration. That’s a total of \(10^{13}\)
log-iterations until it’s learned, which R helpfully tells me is Inf
iterations. I don’t want to wait for that.
I suspect there’s a flaw in the evaluation strategy that generated the data in this section13 The nuance lies in the idea of “a large enough number of candidates” – I hard-coded this to five, which is probably not large enough for large vocabularies! It may also be the cause of it over-estimating the learning rate for small vocabularies., and that the network actually learns faster than that. These investigations may end up in a separate article.
Useful links
Here are the references I consulted most often regarding building neural networks: