Queueing Systems 2: Percentiles and Simulation
In response to the previous article on Markov chains to model queueing systems I received a lot of requests on how to compute percentiles.
I’m happy about that! More people need to realise that the upper percentiles is where it’s at. That’s what you need to know to evaluate most systems. The average is useful for things like capacity planning and resource allocation, but not to determine user experience.
As some of you guessed already, analytically figuring out percentiles for anything but a trivial queueing system is difficult.
For a simple Markovian one-server system with an infinite-capacity queue11 M/M/1 in Kendall notation. we can do it without blinking. The distribution of response times is exponential with rate \(\mu(1 - R)\), where \(\mu\) is the processing rate, and \(R\) is arrival rate divided by processing rate. From that exponential distribution, we can solve for whatever percentiles we need: Wikipedia helpfully tells us that we get the response time quantile \(p\) (e.g. 0.95 for 95th percentile) through the formula
\[T_p = \frac{-ln(1 - p)}{\mu(1-R)}.\]
But that’s for a one-server system with infinite-capacity queue – not what we were dealing with.
Analytical Method
The system we were working with looked like
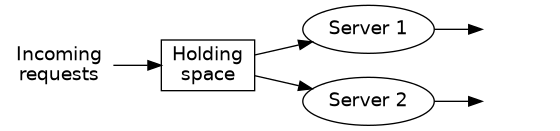
If you need a reminder of how it worked in more detail, please see the introduction in the previous article. For this system, it’s not so easy. In fact, with my analytical skills, I couldn’t find an exact solution. It might exist, but I’m not good enough to find it.
However, let me show you how I got close! Then we’ll see how we can run a simulation to get the same thing.
Response Times In Each State
There are three states in the system above where it accepts new arrivals: \(s_0\), \(s_1\), and \(s_2\). These correspond to when the system is completely idle, when there is one request being processed, and when both servers are busy processing requests.22 If at any point you are confused, read the previous article. It goes into a little more detail on these things.
In the first two of these states, the response time is almost obvious. By definition, in these states, there’s a server free that will immediately pick up the incoming request. In other words, the response time is the service time, and that is exponentially distributed with rate \(\mu\).
It is the third accepting state where we run into trouble. If a request arrives when both servers are busy, the response has to wait for two events to occur: first, one server has to become available. Then that server has to complete processing the request we’re measuring the response time for.
This is one of those cases where it’s really convenient to assume exponential processing times: the memorylessness of the exponential distribution means that we don’t have to care how long the currently processing requests have been processed. It doesn’t matter if they have been running for a second or a minute – their processing time still follows an exponential distribution with rate \(\mu\).
Since we have two servers, and we only need to wait for one of them to be empty, we can exploit another useful property of the exponential distribution: when we have
\[T_1 \sim Exp(\mu)\]
and
\[T_2 \sim Exp(\mu)\]
then
\[min(T_1, T_2) \sim Exp(2\mu).\]
This means that waiting for the smallest of two (independent) identically distributed exponential variables is identical to waiting for a single exponential variable with twice the rate.
So, backing up: a request that arrives to two busy servers need to wait for
\[min(T_1, T_2) + T_3\]
where \(T_1\), \(T_2\), and \(T_3\) are distributed exponentially with rate \(\mu\). We have seen already that this reduces to
\[T_\mathrm{min} + T_3\]
where \(T_\mathrm{min}\) is exponentially distributed with rate \(2\mu\). How is the sum of two exponential variables distributed? This is where I run out of skill. What I do know is that the sum of two identically exponentially distributed variables follow an Erlang-2 distribution. However, these are not identically distributed: one has rate \(2\mu\) and the other has rate \(\mu\).
So what if we cheat a little?
Let’s pretend that both have rate \(1.5\mu\).
This is where all theoreticians fall out of their chair. Can you just do that?
My defense it that I’m an industrial statistician. I don’t need exact answers, I need answers that are good enough to make practical decisions. In this case, getting the processing rate slightly wrong is one of my least worries. There are so many other bigger uncertainties in the problem to be solved, that I just don’t care if the processing rate is slightly off.
So now we have two exponential variables, identically distributed with rate \(1.5\mu\). The sum of those follow an Erlang-2 distribution with rate \(1.5\mu\). Much easier!
State Probabilities
Not all states are equally probable, though. We have to weigh these variables according to the probability of being in each state. Also, since we are looking only at the response time for the requests that are accepted, we need to normalise the probabilities of the first three states so they sum up to one.33 The last state, \(s_3\), does not accept any new requests.
These probabilities, we found out in the last article, are \(\pi_0 = 0.5\), \(\pi_1 = 0.34\), \(\pi_2 = 0.12\). If we normalise these to sum to one, we get instead \(\pi_0 = 0.52\), \(\pi_1 = 0.35\), \(\pi_2 = 0.13\). We combine those with the distributions above, and plug in \(\mu = 110\) from our system, and we get the following distribution for response times:
\[F_T(t) = 1 - (0.52 e^{-110 t} + 0.35 e^{-110 t} + 0.13 (e^{-165 t} + 165te^{-165 t}))\]
We can plot this to get a sense of how the response times are distributed:
If we now want to know a particular response time percentile, we can either look it up visually in a plot like the above, or, for a more exact result, we can solve an equation for it:
\[0.95 = 1 - (0.52 e^{-110 t} + 0.35 e^{-110 t} + 0.13 (e^{-165 t} + 165te^{-165 t}))\]
The solution to this is
\[T_{0.95} \approx 27 \mathrm{ms}\]
Similarly, we have
\[T_{0.99} \approx 42 \mathrm{ms}\]
These are approximations, but it bears repeating: models are not there to be right, only to be useful guides for decisions. I suspect these numbers are close enough to be usable. How can we find out? Let’s verify by simulation!
Simulated Response Time Distribution
We can simulate this queueing system without much fanfare. First, we set up some important variables.
import math import random simulation_step = 0.001 * 0.1 # seconds per step arrival_rate = 75 # events per second processing_rate = 110 # events per second
For simplicity, I decided to go with a simulation that has discrete time steps. The drawback of this is that if our simulated time step is too long, then multiple events can take place in the same time step, some of which are conflicting (e.g. if an arrival and a departure happens in the same time step, which do we consider first?)
I hope that by making the time steps small enough compared to the rates involved, we will have few such conflicts and they will not affect the result too much. In the code above, a time step is defined to be 1/10th of a millisecond. This will trigger our most frequent event (server processing) around 1 % of the time steps. Thus, there is a low risk of collision.44 The cost of this simplicity is increased computational work: with such a low probability of an event occurring at each time step, we are wasting a lot of iterations on time steps where nothing at all happens!
def event_occurs(rate): return random.random() < 1 - math.exp(-rate * simulation_step)
This random function determines, based on rate, whether an event has occurred
this time step or not. Based on the analysis above, we expect this function to
return True only about 1 % of the time. More specifically, this function will
return True on average rate times per second – exponentially
distributed.55 The reader is encouraged to run the function many times and
plot the result to confirm this!
Then we move on to the simulation logic.
Quite arbitrarily, I decided that the holding space gets its own variable, and the servers share a list. It could have been done any other way, but this was the one I happened to choose.
Again, to keep things simple, the number stored in these places is the age of
the simulated request that sits there. So, for example, if servers[1] is equal
to 0.0023, then we know that the request currently being processed by the second
server has been in the system for 2.3 ms.
def simulate_time(seconds): # Number indicates how long request has been there. -1 means idle. holding_space = -1 servers = [-1, -1] # Simulate desired time. for t in range(0, int(1/simulation_step*seconds)): # Attempt arrival. if event_occurs(arrival_rate) and holding_space == -1: holding_space = 0 for (i, server) in enumerate(servers): if server >= 0: # Attempt to complete processing. Otherwise age request. if event_occurs(processing_rate): # Report back the response time for this request. yield server servers[i] = -1 else: servers[i] += simulation_step else: # Pick from holding space if server is available. servers[i] = holding_space holding_space = -1 # Age any request in the holding space if not picked by now. if holding_space >= 0: holding_space += simulation_step
This main body of the simulation ought to be fairly well explained by the comments. We first check if an arrival occurs. If it does, and the holding space is empty, we insert a request of age 0 into the holding space.
For both servers, we check first if they are busy processing a request, and if they are, we see if they are finished. If they are, we report the final response time for that request and set the server to idle. If they weren’t finished, we age the request they are processing. If a server was not busy to begin with, and there was a request in the holding space, it gets picked up by that server. Then we age the request in the holding space, if there is one there.66 It might seem like the order in which we do these things is significant, but the idea is that we should have picked a time step small enough that only one of the things that can happen do happen in any one time step, thus making the order unimportant.
Finally, we can define a function to get various percentiles from the distribution of response times we get from the simulation:
def quantile(values, a): values = sorted(values) return values[math.ceil(len(values)*a)] # Simulate 60 seconds. response_times = list(simulate_time(60)) print(f'95 %: {quantile(response_times, 0.95)*1000:.0f} ms') print(f'99 %: {quantile(response_times, 0.99)*1000:.0f} ms')
95 %: 28 ms 99 %: 43 ms
The exact numbers above will vary each time I publish this article due to the randomness involved in the simulation, but generally, they seem to be very close to the numbers we got analytically. That makes me more confident that the approximation I picked was appropriate.
Replicating Simulation
If we want to know how close our simulated percentiles are to the true values, we can repeat the simulation a few times to get a sense of the variation involved:
# Simulate 60 seconds a few times, get 95th percentile for each. p99s = sorted([quantile(list(simulate_time(60)), 0.95) for _ in range(0, 12)]) print(', '.join(f'{p99*1000:.0f}' for p99 in p99s))
27, 27, 28, 28, 28, 28, 28, 28, 28, 29, 29, 29
It certainly looks like we’re onto something.